通项公式
众所周知,给定如下递推式,计算$a_{n}的值是多少$
OIer的标准解法显然是递推模拟
#include <iostream>
using namespace std;
int recursive_a(int n) {
if (n == 1) return 2;
if (n == 2) return 1;
return recursive_a(n-1) + 2 * recursive_a(n-2);
}
int main() {
int n;
cout << "Enter n: ";
cin >> n;
cout << "a_" << n << " = " << recursive_a(n) << endl;
return 0;
}或者说最常见的数组递推,也可以说是DP的一种
#include <iostream>
#include <vector>
using namespace std;
int dp_a(int n) {
if (n == 1) return 2;
if (n == 2) return 1;
vector<int> dp(n+1);
dp[1] = 2;
dp[2] = 1;
for (int i = 3; i <= n; ++i) {
dp[i] = dp[i-1] + 2 * dp[i-2];
}
return dp[n];
}
int main() {
int n;
cout << "Enter n: ";
cin >> n;
cout << "a_" << n << " = " << dp_a(n) << endl;
return 0;
}甚至还有空间优化解法
#include <iostream>
using namespace std;
int optimized_a(int n) {
if (n == 1) return 2;
if (n == 2) return 1;
int a = 2, b = 1, c;
for (int i = 3; i <= n; ++i) {
c = b + 2 * a;
a = b;
b = c;
}
return b;
}
int main() {
int n;
cout << "Enter n: ";
cin >> n;
cout << "a_" << n << " = " << optimized_a(n) << endl;
return 0;
}或者数学系犇犇们也可能很快得到了优化解法,高中求解通项公式的方法,学过线性代数的直接用特征根法,解出通项公式,直接$O(1)$,完美撒花。
#include <iostream>
#include <cmath>
using namespace std;
// 通项公式计算(O(1)时间/空间复杂度)
int closed_form(int n) {
return pow(2, n) - pow(-1, n);
}
int main() {
int n;
cout << "输入n值:";
cin >> n;
cout << "通项公式结果:a_" << n << " = " << closed_form(n) << endl;
return 0;
}但是我想顺利深挖一下线性代数角度怎么理解的。
特征根
线性代数,顾名思义,研究的是向量,而代数学研究的是代数。因此为什么线性代数就是和矩阵过不去,因为线性代数,小名矩阵。
我们可以用线性代数的视角,将$a_{n}看作是一个无穷维的向量\overrightarrow{a}$,我们已知两个初始值,那么这个矩阵为$\bigl[\begin{smallmatrix} 2 \ 1 \end{smallmatrix}\bigr]$,这个矩阵的秩为2,因此我们需要构造另一个向量$\overrightarrow{q_1}$来和$\overrightarrow{a}$形成基底。
那么等比数列$q^n$ 是一个优秀的基底,这种数列的好处是,我们可以轻松的找出它任意一项的数值,你只需要把它代入指数就行,我们只需要把$n$的结构代入等比数列
$$q^n = 2q^{n-2} + q^{n-1}$$
$$\frac{q^n}{q^{n-2}} = 2 + \frac{q^{n-1}}{q^{n-2}}$$
$$q^2 - q - 2 = 0$$
很自然的,我们推导出了特征根方程给出的答案
$$q_1 = 2,q_2 = -1$$
那么$\overrightarrow{q_1} = \bigl[\begin{smallmatrix} 2^0 \ 2^1 \ 2^3 \ ... \end{smallmatrix}\bigr]$,$\overrightarrow{q_2} = \bigl[\begin{smallmatrix} (-1)^0 \ (-1)^1 \ (-1)^3 \ ... \end{smallmatrix}\bigr]$
通过观察我们可以发现,$\overrightarrow{q_1} + \overrightarrow{q_2} = \overrightarrow{a}$,即
$$\bigl[\begin{smallmatrix} 1 \ 2 \end{smallmatrix}\bigr] + \bigl[\begin{smallmatrix} 1 \ -1 \end{smallmatrix}\bigr] = \bigl[\begin{smallmatrix} 2 \ 1 \end{smallmatrix}\bigr]$$
所以$a_n的通项公式是q_1 + q_2$,即
$$2^n + (-1)^n$$
如果要求$a_{10000}$的值,那显然就是$O(1)$的速度$2^{10000} + 1$

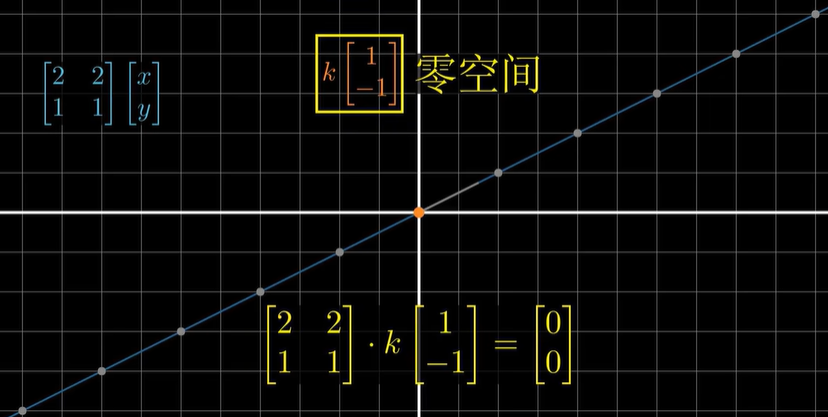















这一切,似未曾拥有