动态规划的核心思想是将复杂问题分解为简单的子问题，并通过存储子问题的解来避免重复计算，从而节省计算时间。动态规划通常适用于满足以下两个条件的问题：

最优子结构（Optimal Substructure）：一个问题的最优解可以由其子问题的最优解构成。
重叠子问题（Overlapping Subproblems）：问题可以分解为许多重复的子问题，而这些子问题的解会被多次利用。

解决动态规划问题时，通常遵循以下步骤：

1. 定义状态（State）
首先，我们需要定义一个状态，用来描述问题的子结构。在实际操作中我们通常会定义一个数组或表格来存储子问题的结果。要注意状态的定义应该尽量简单，但又能包含足够的信息来从中推导出最终的解。

2. 确定状态转移方程（State Transition Equation）
状态转移方程是解决动态规划问题的关键，它描述了如何从一个子问题的解推导出更大问题的解。状态转移方程通常是递推公式，能够根据已解决的子问题来构造当前问题的解。

3. 确定边界条件（Base Case）
对于最小的子问题（也就是递归的基础情形），需要明确给出其解，这些就是边界条件。在实现时，这些边界条件是动态规划算法的起点，通常是一些初始值。。

4. 填表（Table Filling）或递归计算
自底向上：通过循环填充表格（通常是二维数组或一维数组），从最小的子问题开始，逐步计算出最终的解。
自顶向下：通过递归调用子问题，并使用备忘录（Memoization）存储已计算的结果，避免重复计算。

01背包问题

求解目标：

有$n$件物品和一个容量为$v$的背包。
第$i$件物品的费用是$\text{c}[i]$，价值是$\text{w}[i]。$
求解将哪些物品装入背包可使价值总和最大。

这是最基础的背包问题，特点是：每种物品仅有一件，可以选择放或不放。

用子问题定义状态：即$f[i][v]$表示前$n$件物品恰放入一个容量为$v$的背包可以获得的最大价值。则其状态转移方程便是：

$$f(i,j) = \max(f(i-1,j), f(i,j-\text{save}[i]) + \text{value}[i])$$

这个方程非常重要，基本上所有跟背包相关的问题的方程都是由它衍生出来的。所以有必要将它详细解释一下：

“将前$i$件物品放入容量为$v$的背包中”这个子问题，若只考虑第$i$件物品的策略（放或不放），那么就可以转化为一个只牵扯前$i-1$件物品的问题。
如果不放第$i$件物品，那么问题就转化为“前$i-1$件物品放入容量为$v$的背包中”，价值为$f[i-1][v]$；
如果放第$i$件物品，那么问题就转化为“前$i-1$容量为$\text{v}-c[i]$的背包中”，此时能获得的最大价值就是$\text{f}[i-1][v-c[i]]$再加上通过放入第i件物品获得的价值$w[i]$。

#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;

const int maxn = 2e4 + 10;
int w[maxn];
int dp[maxn][maxn];

int main()
{
    int v, n;
    cin >> v >> n;
    for (int i = 1; i <= n; i++)
        cin >> w[i];
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= v; j++)
        {
            if (j < w[i])
                dp[i][j] = dp[i - 1][j];
            else
                dp[i][j] = max(dp[i - 1][j],dp[i - 1][j - w[i]] + w[i]);
        }
    }

    cout << v - dp[n][v] << endl;

    return 0;
}

导弹拦截

某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。
输入导弹依次飞来的高度（雷达给出的高度数据是$50000≤50000$的正整数），计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

输入格式
11行，若干个整数（个数$100000≤100000$）
输出格式
22行，每行一个整数，第一个数字表示这套系统最多能拦截多少导弹，第二个数字表示如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

将拦截的导弹的高度提出来成为原高度序列的一个子序列，根据题意这个子序列中的元素是单调不增的（即后一项总是不大于前一项），我们称为单调不升子序列。本问所求能拦截到的最多的导弹，即求最长的单调不升子序列。

考虑记$dp_{i}$表示「对于前$i$个数，在选择第$i$个数的情况下，得到的单调不升子序列的长度最长是多少」。于是可以分两种情况：

第$i$个数是子序列的第一项。则$dp_{i}$ ← 1。
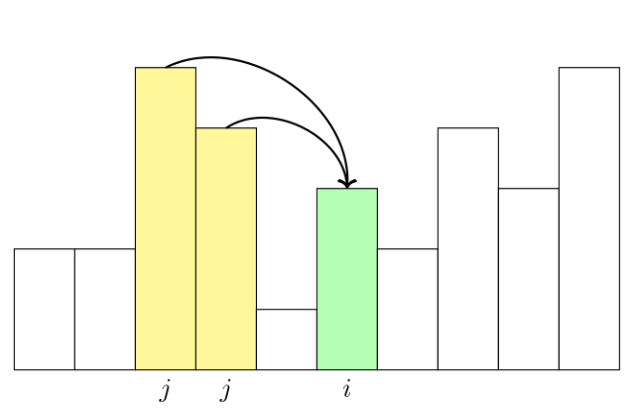
第$i$个数不是子序列的第一项。选择的第$i$数之前选择了第$j$个数。根据题意，第$j$个数的值$h(j)$应当小于第$i$个数的值$h(i)$。枚举这样的$j$，可以得到状态转移方程：

$$ dp_{i} = \max_{\substack{j < i \\ h(j) \geq h(i)}} \left( dp_{j} + 1 \right) $$

综合这两种情况，得到最终的状态转移方程：

$$ dp_{i} = \max_{\substack{j < i \\ h(j) \geq h(i)}} \left(1,dp_{j} + 1 \right) $$

值得注意的是，第$n$个数不一定是最长单调不升子序列的最后一项。为了求出答案，我们需要枚举最后一项是哪个：

$$ans = \max_{1 \leq i \leq n} (dp_i)$$

直接枚举进行状态转移，时间复杂度显然是$O(n)$

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;

const int maxn = 1e5 + 10;
int a[maxn];
int dp_1[maxn];
int dp_2[maxn];

int main()
{
    int n = 0;
    int cnt_1 = 1;
    int cnt_2 = 1;
    //cin >> n;
    //for (int i = 1; i <= n; i++)
    //  cin >> a[i];
    while (cin >> a[n])n++;
    dp_1[1] = a[1];
    dp_2[1] = a[1];
    for (int i = 2; i <= n; i++)
    {
        if (a[i] <= dp_1[cnt_1])
            dp_1[++cnt_1] = a[i];
        else
        {
            int pos_1 = upper_bound(dp_1 + 1, dp_1 + 1 + cnt_1, a[i], greater<int>()) - dp_1;
            dp_1[pos_1] = a[i];
        }
        if (a[i] > dp_2[cnt_2])
            dp_2[++cnt_2] = a[i];
        else
        {
            int pos_2 =upper_bound(dp_2 + 1, dp_2 + 1 + cnt_2, a[i]) - dp_2;
            dp_2[pos_2] = a[i];
        }
    }
    cout << cnt_1 << endl << cnt_2 << endl;

    return 0;
}