福兮祸兮

高中生涯最后一次参加信竞了，今年的计算量特别大，奈何数学特别差，突击检查我两位数加减法，我还得掰一掰手指头的那种。你要说靠这玩意升学，我想还是算了，我不是什么天才，也没什么天赋，和诸多OIer相比，我起步晚且数理功底差。我们这种小城市里的尘埃，远不及一线城市的OIer，没有导师也没有资源，只依靠着一丝年少轻狂支撑，我想路至此已到尽头，未来能凭借一腔热血能做成的事越来越少了，到此为止，给自己一个完美的落幕吧。
一个人从枚举学到图论，实在是步步维艰，没有朋友，没有导师，在我们这个小地方的高中是一件及其孤独的旅程。在这样一个充满质疑的环境中，高考的压力令人暗自神伤，我不想放弃竞赛，可是一人独行就要承受一切。一个普通人想要走上去实在太难，失败了会遭受高考压力的嘲讽，最终陷入两难，苦苦挣扎于高考，却又不甘心放弃。本该给高考100%的精力，却分给了50%的竞赛，最后飞扬三年，黯淡收场，我真的错了吗。

选择题

1.在 Linux 系统终端中，用于列出当前目录下所含的文件和子目录的命令为（）。
A. ls B. cd C. cp D. all
ls 命令用于显示指定工作目录下之内容（列出目前工作目录所含之文件及子目录)。
cd 命令用于切换当前工作目录。
cp 命令主要用于复制文件或目录。
all 我也不知道这干啥。

故选 A 。

2.二进制数 $00101010$ 和 $00010110$ 的和为（）。
A. 00111100 B. 01000000 C.00111100 D. 01000010
计算题
$1+1=10,0+0=0,1+0=1$
算出来是
$01000000_{2}$
故选 B 。

3.在程序运行过程中，如果递归调用的层数过多，可能会由于（）引发错误。
A. 系统分配的栈空间溢出
B. 系统分配的队列空间溢出
C. 系统分配的链表空间溢出
D. 系统分配的堆空间溢出
递归的时候是像栈一样，先进后出的。
故选 A 。

4.以下排序方法中，（）是不稳定的。
A. 插入排序 B. 冒泡排序 C. 堆排序 D. 归并排序
补充不稳定是什么：
比如$2$个值，第$x$个数字是$z$，第$y$个数值也是$z$ 。其中不妨设$x<y$ 。但是某些不稳定的排序后可能会出现$x$排到$y$后面的情况。
故选 C 。

5.以比较为基本运算，对于 $2n$ 个数，同时找到最大值和最小值，最坏情况下需要的最小的比较次数为（）。
A.$4n-2$ B.$3n+1$ C.$3n-2$ D.$2n+1$
把序列分成两半，长度分别为 $n$。两两之间比，小的和最小值比，大的和最大值比。其中两组第一个数只要比一次。
所以$1+3×(n-1)=3n-2$

6.现有一个地址区间为 $0$ 到 $10$ 的哈希表，对于出现冲突情况，会往后找第一个空的地址存储（到 $10$ 冲突了就从 $0$ 开始往后），现在要依次存储$(0,1,2,3,4,5,6,7)$,哈希函数为$h(x) = x^2 mod 11$,请问 $7$ 存储在哈希表哪个地址中（）。
A. 5 B. 6 C. 7 D. 8
每个都算一下。分别为0,1,4,9,5,3,3,5
重复的调整一下,0,1,4,9,5,3,6,7

故选 C 。

7.G 是一个非连通简单无向图（没有自环和重边），共有 $36$ 条边，则该图至少有（）个点。
A. 8
B. 9
C. 10
D. 11

设有 $n$ 个点，除了一个孤立点外剩下点为完全图。

$\frac{1}{2}×(n-1)(n-2)=36$
解得 $n=10$
故选 C 。

8.令根结点的高度为 1，则一棵含有 2021 个结点的二叉树的高度至少为（）。
A. 10
B. 11
C. 12
D. 2021

“至少”，故是完全二叉树。
所以 $2^{10}≤2021<2^{11}$

故选 B 。

9.前序遍历和中序遍历相同的二叉树为且仅为（）。
A. 只有 1 个点的二叉树
B. 根结点没有左子树的二叉树
C. 非叶子结点只有左子树的二叉树
D. 非叶子结点只有右子树的二叉树
前序遍历：中左右。
中序遍历：左中右。
所以去掉左时两个相同，选择 D 。

10.定义一种字符串操作为交换相邻两个字符。将DACFEB变为ABCDEF最少需要（）次上述操作。
A. 7 B. 8 C. 9 D. 6

考虑冒泡排序思想。ADCFEB1次，ABDCFE4次，ABCDFE1次，ABCDEF1次。

共 7 次。

故选 A 。

11.有如下递归代码

solve(t, n):
if t=1 return 1
else return 5 * solve(t-1,n) mod n

则 solve(23,23) 的结果为（）。
A. 1
B. 7
C. 12
D. 22
阅读可得，要求$5^{23}-1mod23$
考虑用费马小定理，因为 $23$ 是质数，所以$5^{22}≡1(mod23)$

13.有 8 个苹果从左到右排成一排，你要从中挑选至少一个苹果，并且不能同时挑选相邻的两个苹果，一共有（）种方案。
A. 36 B. 48 C. 54 D. 64

$f_{i }=f_{i-1}+f_{i-2}$

$f_{8}=55$

$f_{8}-1=54$

故选 C

14.设一个三位数 $n=\Delta A B C$ 其中 $a,b,c$ 均为 1 到 9 之间的整数，若以 $a,b,c$ 作为三角形的三条边可以构成等腰三角形（包括等边），则这样的 $n$ 有（）个。

A. 81 B. 120 C. 165 D. 216

故选 C 。

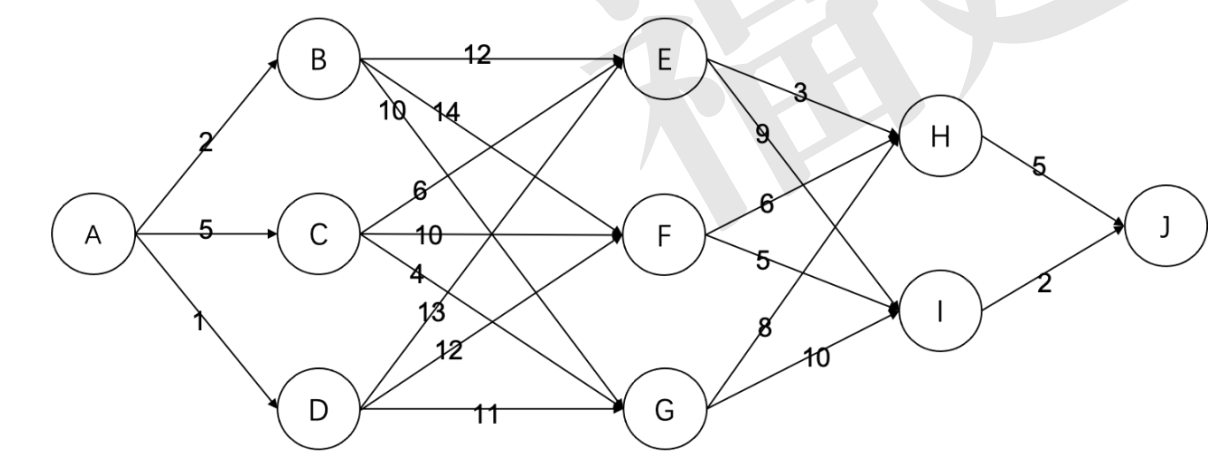
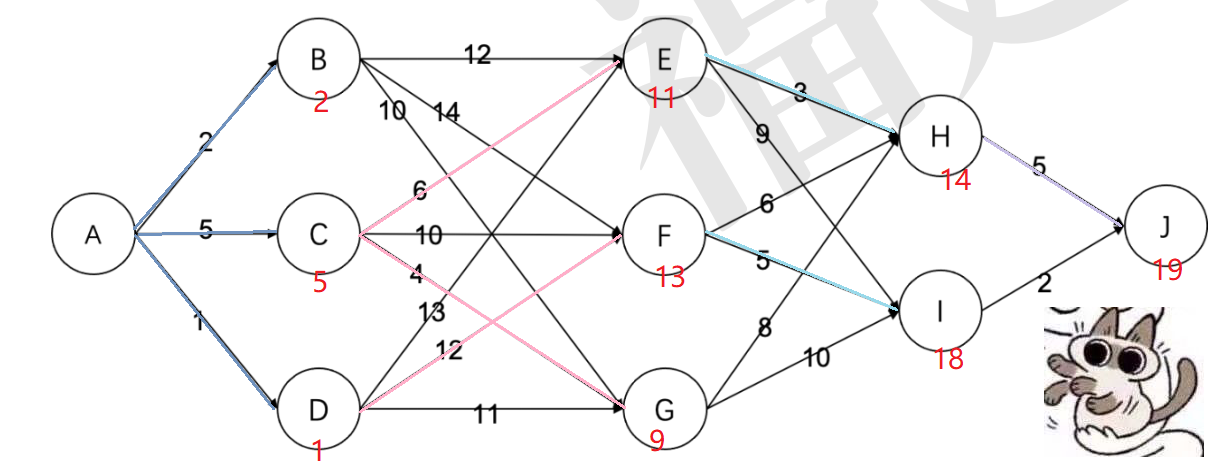
15.有如下的有向图，节点为 A, B, … , J, 其中每条边的长度都标在图中。则节点 A 到节点 J 的最短路径长度为（）。

A. 16 B. 19 C. 20 D. 22

考虑模拟 dijkstra 。

故选 B 。

2021CSP-S信息学奥赛

福兮祸兮

选择题

填空题